Thursday, November 25, 2010

Sorting

from wikipedia:

Name Best Average Worst
 Memory Stable Method
 Other notes
Insertion sort \mathcal{} n \mathcal{} n^2 \mathcal{} n^2 \mathcal{} {1} Yes Insertion Average case is also 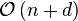\mathcal{O}\left( {n + d} \right), where d is the number of inversions
Binary tree sort — 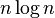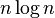\mathcal{} {n \log n} \mathcal{} {n \log n} \mathcal{} n Yes Insertion When using a self-balancing binary search tree
Cycle sort — \mathcal{} n^2 \mathcal{} n^2 \mathcal{} {1} No Insertion In-place with theoretically optimal number of writes
Selection sort \mathcal{} n^2 \mathcal{} n^2 \mathcal{} n^2 \mathcal{} {1} No Selection Its stability depends on the implementation. Used to sort this table in Safari or other Webkit web browser [2].
Bubble sort \mathcal{} n \mathcal{} n^2 \mathcal{} n^2 \mathcal{} {1} Yes Exchanging Tiny code
Merge sort 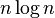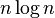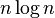\mathcal{} {n \log n} \mathcal{} {n \log n} \mathcal{} {n \log n} Depends Yes Merging Used to sort this table in Firefox [3].
Quicksort 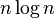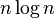\mathcal{} n \log n \mathcal{} n \log n \mathcal{} n^2 \mathcal{} \log n Depends Partitioning Can be implemented as a stable sort depending on how the pivot is handled. Naïve variants use 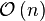\mathcal{O} \left( n \right) space
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)